스택
가장 큰 특징 :
LIFO
마지막에 넣은 게 가장 먼저 나온다
문제를 풀이하면서 가장 중요한 건
스택을 어떤 용도로 사용하고.
어떤 경우에 push를 하고,
어떤 경우에 pop을 해야 할까? 를 생각해야 된다.
문제풀이
11052 - 카드 구매하기 (실버1) : https://www.acmicpc.net/problem/11052
풀이 :
N개의 카드를 구매하기 위해 지불할 수 있는 금액의 최댓값을 구하는 문제.
전형적인 dp(다이나믹 프로그래밍) 문제이며,
N의 범위가 10^3으로 시간복잡도가 O(N^2)일 때 10^6으로 제한시간 내에 충분히 가능하다.
가장 쉬운 방법으로는 가능한 모든 경우의 수를 구하여 값 중 최댓값을 구하는 것이다.
하지만 같은 카드를 구매하는 경우에서 굳이 적은 비용을 낼 필요가 없다.
-> 카드를 i개 구매할 때 필요한 금액 중 최댓값을 dp[i]에 저장.
->ex)
dp[1] = p[1]
dp[2] =p[1] + dp[1] or dp[2] //중 최댓값
, ... ,
dp[k] = p[1] + dp[k-1], p[2] + dp[k-2], ... , dp[k] // 최댓값
#include <iostream>
#include <algorithm>
using namespace std;
int p[1001];
int db[1001];
int main(void) {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> p[i];
db[i] = p[i];
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
db[i] = max(db[i], p[j] + db[i-j]);
}
}
cout << db[n];
}
16194 - 카드 구매하기 2 (실버1) : https://www.acmicpc.net/problem/16194
풀이 :
앞의 문제에서는 최댓값을 구했으나, 최솟값을 구하는 문제 // 부등호만 다르게 해 주면 되는 문제.
//위 코드에서 max->min 으로만 해도 AC
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> v(n + 1);
for (int i = 1; i <= n; ++i)
cin >> v[i];
for (int i = 1; i <= n; ++i) {
for (int a = 1; a < i/2+1; ++a) {
if (v[i] > v[a] + v[i - a])
v[i] = v[a] + v[i - a];
}
}
cout << v[n];
}
16909 - 카드 구매하기 3 (플3) : https://www.acmicpc.net/problem/16909
풀이 : (문제를 풀 때 생각의 흐름으로 정리해 봤습니다 ^^;;)
카드를 구매하는 방법이 연속된 카드만 구매할 수 있으며, 가격은 그 카드 중 최댓값에서 최솟값을 뺀 가격이다. 가능한 모든 방법에 대한 가격의 합을 구하는 문제.
가능한 모든 방법의 수 = N개 일 때, N(N+1)/2
∵ 1개 선택한 방법 : N, 2개 선택한 방법 : N-1, ... , K개 선택한 방법 : N-k+1, ... , N개 선택한 방법 : 1개
이때 N의 범위가 10^6까지 이므로 시간복잡도O(N^2)인 방법으로 할 경우 시간초과가 뜨게 된다.
또한 자료형의 범위가 10^6이므로 모든 방법에서 가격이 최대일 때, 정답은 10^18이 된다.
고로 약 -9*10^18 ~ 9*10^18 까지 저장할 수 있는 long long 형을 사용하여 합을 구해야 된다.
모든 방법을 구하지 않고 모든 방법의 가격의 합을 구하려면 어떻게 해야 될까?,,
먼저 문제를 두 개로 나누어서 단순화해보자.
1. 모든 방법의 최댓값의 합, 2. 모든 방법의 최솟값의 합을 구하는 두 개의 문제로 나누어 푼 다음.
마지막 출력에서 두 개의 차를 구하면 된다!
1. 모든 방법의 최댓값의 합을 구하기.
먼저 머릿속으로 정리되지 않으니, 직접 가격을 구하는 모든 방법을 써보자.
가장 쉬운 방법인 모든 방법의 최댓값을 구하고, 중복된 연산을 파악하면 될 거 같다.
입력 :
10
2 5 1 2 10 2 3 5 4 1
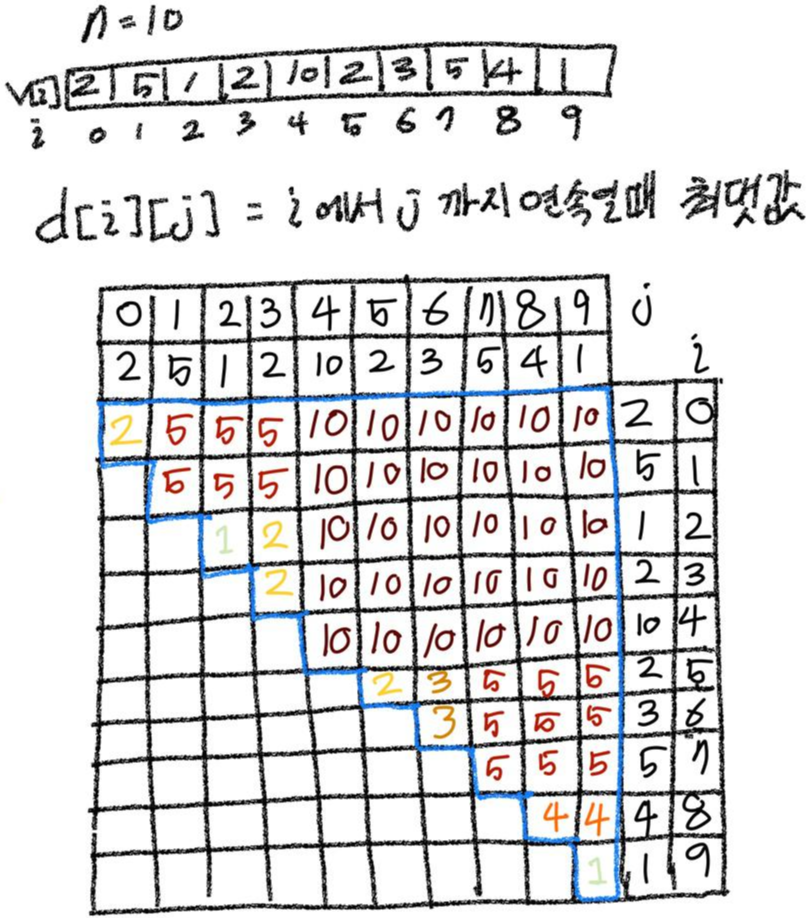
여기서 최댓값을 보면 직사각형 모양으로 되어있다. 각 직사각형의 세로, 가로길이를 구해보자.
i번째 세로의 길이에 영향을 주는 요인
1. 0~i-1 값 중에 자신보다 큰 값이 있는지
예를 들어 10(i=4)일 때, i가 0부터 3중에서 값이 10보다 큰 것은 없다, -> 세로길이는 i+1
5(i=7)일 때, i가 0부터 6중에서 10(i=4) 자신보다 크다. -> 세로길이는 i-(자신보다 큰값의 번호)
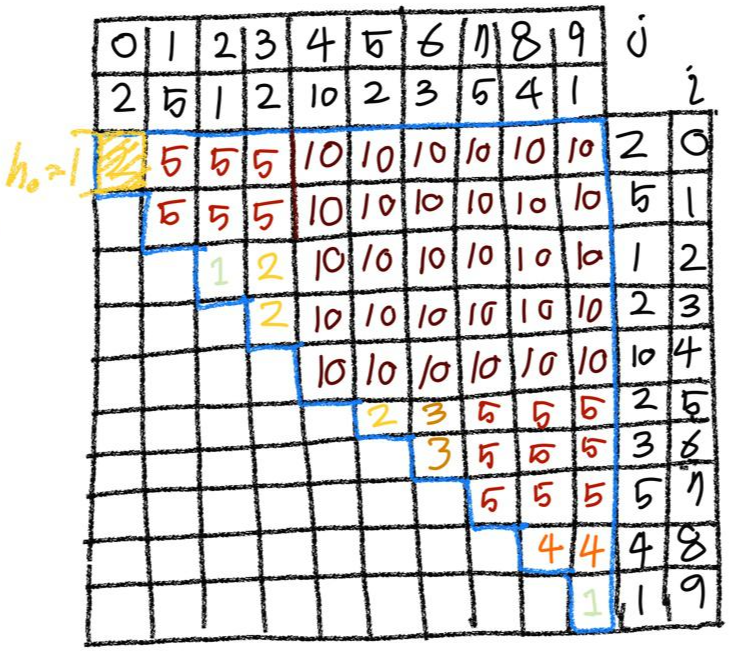





(같은 방식의 세로길이 구하는 방법 일부 생략..)
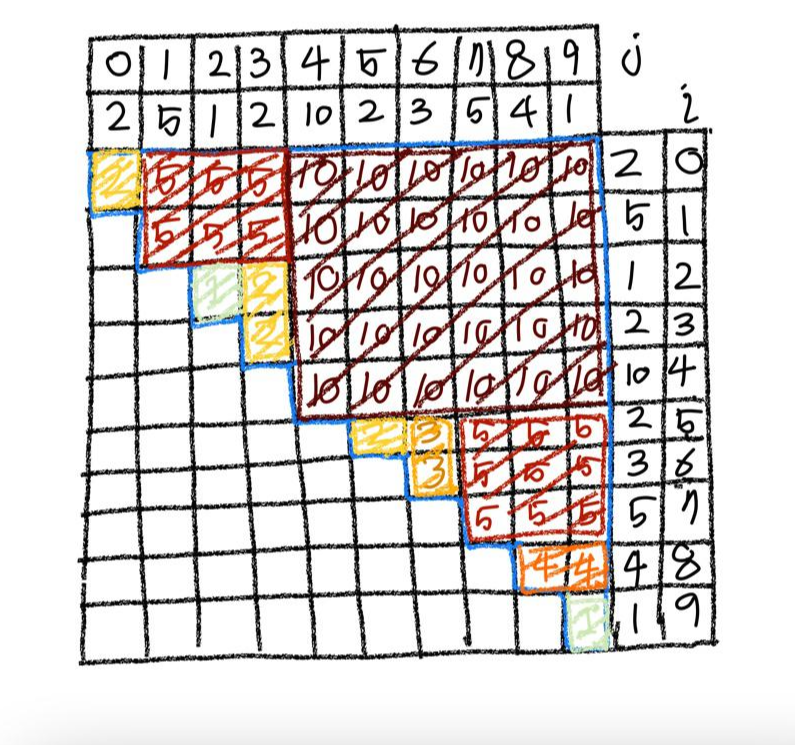
여기서 k의 세로길이는 top도 아니고 upper_bound도 아니다.
k의 세로 길이 =
자신이 최댓값일 경우
i+1
자신이 최댓값이 아닌 경우
k - [0, k)에서 k의 값 보다 큰 값 중 번호가 가장 큰 번호
으로 예측할 수 있다. (이후 반례를 생각해 보았으나 반례가 없으므로 맞다고 예측한다.)
k번째 세로 길이를 구하는 알고리즘
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
// now의 세로길이 - ([0, now]에서 now 보다 큰값 중 i가 가장 큰수)
// 자신이 제일 크다면 now의 세로길이
vector<int> nowH(1000001);
vector<int> v(1000001);
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n;
long long ans=0;
cin >> n;
for (int i = 0; i < n; ++i)
cin >> v[i];
stack<pair<int, int> >st;
for (int i = 0; i < n; ++i) {
while (!st.empty() && st.top().first <= v[i]) st.pop();
if (!st.empty())
nowH[i] = i - st.top().second;
else
nowH[i] = i + 1;
st.push({ v[i], i });
cout << nowH[i] <<" ";
}
}
/*
input :
10
2 5 1 2 10 2 3 5 4 1
output :
1 2 1 2 5 1 2 3 1 1
*/
비슷한 방법으로 최댓값의 가로길이, 최솟값의 세로, 가로길이를 구할 수 있다.
// 합을 구할 땐 자료형에 좀 더 신경 써주자...^^
//16909 풀이
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
long long n;
vector<int> nowH(1000001), nowW(1000001);
vector<int> v(1000001);
void f(bool pos1, bool pos2) {
stack<pair<int, int> >st;
if (pos1) {
for (int i = 0; i < n; ++i) {
if (pos2)
while (!st.empty() && st.top().first <= v[i]) st.pop();
else
while (!st.empty() && st.top().first >= v[i]) st.pop();
if (!st.empty())
nowH[i] = i - st.top().second;
else
nowH[i] = i + 1;
st.push({ v[i], i });
}
}
else {
while (!st.empty()) st.pop();
for (int i = n - 1; i >= 0; --i) {
if (pos2)
while (!st.empty() && st.top().first < v[i]) st.pop();
else
while (!st.empty() && st.top().first > v[i]) st.pop();
if (!st.empty())
nowW[i] = st.top().second - i;
else
nowW[i] = n - i;
st.push({ v[i],i });
}
}
}
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
long long ans = 0;
cin >> n;
for (int i = 0; i < n; ++i)
cin >> v[i];
f(1, 1);
f(0, 1);
for (int i = 0; i < n; ++i)
ans += (long long)v[i] * ((long long)nowH[i] * nowW[i]);
f(1, 0);
f(0, 0);
for (int i = 0; i < n; ++i)
ans -= (long long)v[i] * ((long long)nowH[i] * nowW[i]);
cout << ans << endl;
}
풀이 2:
모든 위치 i에 대해서
그 위치가 (최댓값이 되는 구간의 개수)*A[i] - 최솟값이 되는 구간의 개수*A[i]
를 모두 더한값이 문제의정답이 된다.
now를 최댓값으로 갖는 위치 찾기.
총 k개의 수가 포함되어 있다면, 구간의 개수는 k*(K+1)/2 - 왼쪽구간(왼쪽에서 시작해서 왼쪽에서 끝나는), 오른쪽 구간(오른쪽 에서 시작해서 오른쪽 에서 끝나는)
left[i], right[i]구하기
a[i]가 최댓값인 범위.
// 히스토그램에서 가장 큰 직사각형 찾는 것과 유사하게 할 수 있다.
'Algorithm > Intermediate' 카테고리의 다른 글
| 문자열 매칭 알고리즘[1](라빈 카프)[String Searching Algorithm, Rabin-Karp] (0) | 2021.10.31 |
|---|---|
| 벡터의 활용(Vector, C++) (0) | 2021.10.16 |
| 이진 검색 트리(Binary Search Tree, priorty queue, set, map) (0) | 2021.10.02 |
| 유니온 파인드[Union Find] (0) | 2021.10.02 |
| 스택 중간난이도 문제 풀이(Stack PS) (0) | 2021.10.01 |

