그리디 알고리즘(Greedy Algorithm)
어떤 걸 결정해야 될 때, 그 순간 가장 좋다고 생각하는 것을 계속 선택해나가는 알고리즘
그때그때는 최적일지도 있지만, 최종적으로는 답이 최적이 아닐 수도 있다.
동적 프로그래밍과 같이 쓰이며 서로를 보완한다.
- 그리디 알고리즘의 정의
- 그리디 알고리즘의 특징
- 그리디 알고리즘 문제 풀이 전략
- 그리디 알고리즘 문제 풀이
그리디 알고리즘의 정의
greedy = 탐욕 = 그리디, 욕심쟁이 알고리즘
"매 선택에서 지금 이 순간 당장 최적인 답을 선택하여 적합한 결과를 도출하자"라는 모토를 가지고 있으며,
문제를 해결하는 과정에서 그 순간순간마다 최적이라고 생각되는 결정을 하는 방식으로 진행하여 최종 해답에 도달하는 문제 해결 방식이다.
그리디 알고리즘의 특징
1. 전체 문제해결에서의 최적 해답을 찾지는 못한다.
(∵순간순간마다의 최선의 결정이 전체 문제에서 최선의 해결책이 되지 않기 때문에)
2. 어떻게 보면 가장 쉽다고 생각할 수 있지만 어떻게 보면 가장 어려운 알고리즘이다.
(∵그 순간에 가장 좋다고 생각하는 것을 계속 선택하는 게 최적인지를 증명해야 되기 때문에)
3. 탐욕 선택 속성(greedy choice property), 최적 부분 구조(optimal substrcture) 특성을 가지는 문제들을 해결하는데 강점이 있다.
(=한 번의 선택이 다음 선택에는 전혀 무관한 값이어야 하며 매 순간의 최적해가 문제에 대한 최적해여야 한다는 의미이다. 즉, 지금 이 순간에 최적인 것이 항상 최적일 경우.)
4. 가장 큰 장점은 계산속도이다.
(그리디 방법이 통하는 몇몇의 문제에서는 최적해를 빠르게 산출해낼 수 있다.)
그리디 알고리즘 문제 풀이 전략
그리디 알고리즘은 탐욕 선택 속성(greedy choice property), 최적 부분 구조(optimal substrcture) 특성을 가지는 문제에 해결하는 것에 강점이 있는 특징을 사용하여 문제를 쪼개어 푼다. 즉, 부분 문제에 대한 최적 해결방법이 문제의 최적 해결방법이 될 수 있도록 문제를 변형한다.
문제 접근 방법 :
1. 이 문제는 그리디 방법이 최적이 아니다. -> 반례가 있을 경우 그리디 방법이 아니라는 것을 증명할 수 있다.
2. 이 문제는 그리디 방법이 최적이다. -> 그리디 방법이 맞다는 것은 수학적 증명이 필요하다.
그리디 방법 증명 방법중 한 가지는 아래와 같다.
이 그리디 방법이 정답이다. 왜냐면 여기서 변화를 주었을 때, 본래의 답보다 최적화되어있지 않다.
즉, 중간에 임의의 순서를 바꿨을 때, 정답이 더 최적화되면 안 된다. 정답이 최적화되지 않아야 한다.
S가 `S보다 더 최적화되어있다.
그리디 알고리즘은 한 번 내린 선택이 이후에 뒤집혀서 더 나은 해결책이 나올 수 없는 상황을 전제로 한다. 매 단계에서 가장 최적의 선택을 하기 때문에, 임의로 중간에 순서를 바꾼다거나 혹은 다른 방식으로 수정했을 때, 이미 구한 해결책보다 더 나은 해결책이 나와서는 안된다. 이미 그리디 알고리즘이 찾은 최적의 해결책(S)을 수정하거나 바꿨을 때, 그 수정된 상태(S')가 원래 상태(S)보다 더 나은 상태가 될 수 없다.
그리디 알고리즘 문제 풀이
1931 회의실 배정 : https://www.acmicpc.net/problem/1931
나의 문제 생각 과정
1. 일찍 시작하는 회의부터 배정? 반례
2. 회의시간이 짧은 회의부터 진행? 반례
3. 가장 중복이 덜된 회의부터 진행?
4. 가장 빨리 끝나는 회의부터 진행 : 맞다.
시간복잡도 : O(NlogN) : 정렬하는 시간,
#include <cstdio>
#include <vector>
#include <tuple>
#include <algorithm>
using namespace std;
bool comp(const tuple<int, int> & a, const tuple<int, int> & b) {
int a1, a2, b1, b2;
tie(a1, a2) = a;
tie(b1, b2) = b;
if (a2 == b2) {
return a1 < b1;
}else
return a2 < b2;
}
int main(void) {
int n, ans =0, lastnum = 0;
scanf("%d", &n);
vector<tuple<int, int> > v(n);
for (int i = 0; i < n; ++i) {
int n1, n2;
scanf("%d %d", &n1, &n2);
v[i] = { n1, n2 };
}
sort(v.begin(), v.end(), comp);
for (auto a : v) {
int n1, n2;
tie(n1, n2) = a;
if (lastnum <= n1) {
ans++;
lastnum = n2;
//printf("%d %d\n", n1, n2);
}
}
printf("%d\n", ans);
}
11399 ATM : https://www.acmicpc.net/problem/11399
걸리는 시간을 오름차순으로 정렬 -> 이때 항상 최소
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int main(void) {
int n, ans=0;
scanf("%d", &n);
vector<int> v(n);
for (int i = 0; i < n; ++i) {
scanf("%d", &v[i]);
}
sort(v.begin(), v.end());
for (int i=0, sum = 0; i < n; ++i) {
sum += v[i];
ans += sum;
}
printf("%d", ans);
}
2138 전구와 스위치 : https://www.acmicpc.net/problem/2138
양 끝의 스위치는 두 개의 전구에 영향을 주고 나머지 스위치는 세 개의 전구에 영향을 준다.
이를 그림으로 표현하면 이렇다.
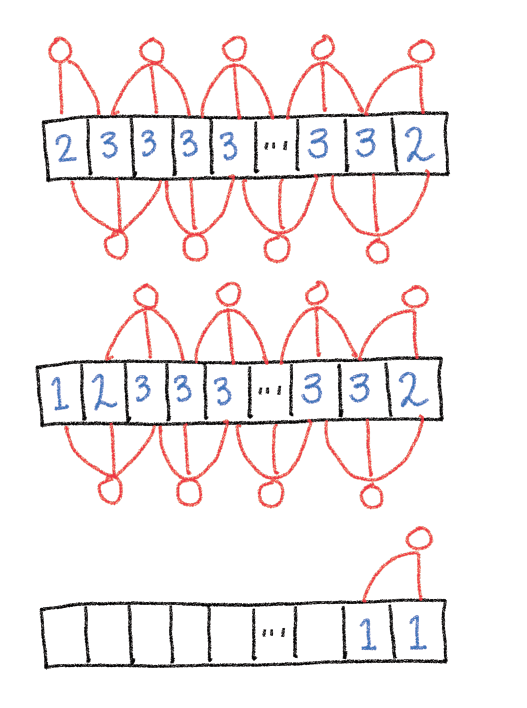
이때 첫 번째 스위치 상태를 결정하면 첫 번째 전구는 두 번째 스위치에게만 영향을 받게 된다.
i번째 전구는 i+1번째 스위치에 의해서만 받게 되는 1대 1 상태를 유지하여 문제를 풀 수 있다.
두 가지 가정으로 나눌 수 있다.
1. 첫 번째 스위치를 눌렀을 경우
2. 첫 번째 스위치를 누르지 않았을 경우
#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <vector>
using namespace std;
int n, ans1 = 0, ans2 = 0;
void f(vector<int>& a, int i) {
if (i - 1 >= 0) a[i - 1] = 1 - a[i - 1];
a[i] = 1 - a[i];
if (i + 1 < n) a[i + 1] = 1 - a[i + 1];
}
int main(void) {
int ans = -1, ans1 =0, ans2 = 0;
scanf("%d", &n);
vector<int> a1(n), a2(n), b(n);
for (int i = 0; i < n; ++i) {
scanf("%1d", &a1[i]);
a2[i] = a1[i];
}
for (int i = 0; i < n; ++i) scanf("%1d", &b[i]);
f(a1, 0);
ans1++;
for (int i = 0; i < n-1; ++i) {
if (a1[i] != b[i]) {
f(a1, i + 1);
ans1++;
}
if (a2[i] != b[i]) {
f(a2, i + 1);
ans2++;
}
}
bool b1= true, b2 = true;
for (int i = 0; i < n; ++i) {
if (a1[i] != b[i]) b1 = false;
if (a2[i] != b[i]) b2 = false;
}
if (b1) ans = ans1;
if (b2) ans = ans2;
printf("%d\n", ans);
}
1285 동전뒤집기 : https://www.acmicpc.net/problem/1285
두 번 뒤집으면 원상태로 돌아가기 때문에 같은 행 또는 열을 두 번 이상 뒤집을 필요가 없다.
순서도 상관이 없다.
20개의 행과 열이 최대로 있을 수 있으니 경우의 수는 2^40, 1조가 넘어 모든 경우를 다 해볼 수는 없다.
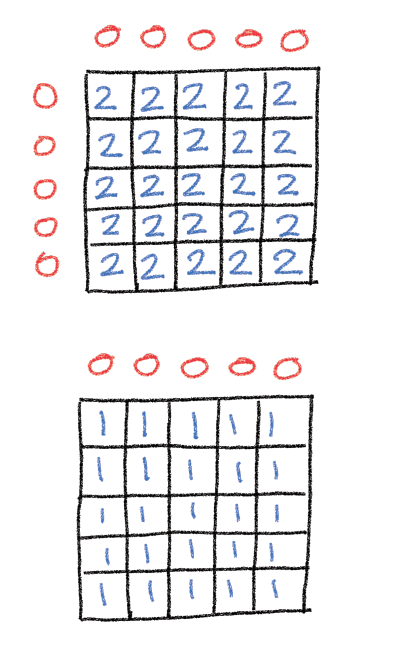
전구와 스위치 문제처럼 각각의 동전을 뒤집을 수 있는 방법의 개수를 표현.
행에 대해서 누를 수 있는 모든 경우의 수(2^20)를 구했을 때, 각각의 열에 의해서 고려 가능.
이 경우 각 열에서 H와 T의 개수를 비교하여 값을 구할 수 있다.
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int n;
int a[21][21], b[21][21]; // H : 0, T : 1
void swapHT(int status, int num) { // status 0 : 행 변환 1 : 열 변환, 행 또는 열 한줄 반대로 저장.
if (status == 0) {
for (int i = 0; i < n; ++i) {
b[num][i] = 1 - b[num][i];
}
} else {
for (int i = 0; i < n; ++i) {
b[i][num] = 1 - b[i][num];
}
}
}
int main(void) {
int ans = 1e9;
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
char ch;
cin >> ch;
if (ch == 'H') a[i][j] = 0;
else a[i][j] = 1;
}
}
for (int i = 0; i < (1<<n); ++i) { //n 조합의 개수 2^n 가지,
memcpy(b, a, sizeof(b));
for (int j = 0; j < n; ++j) { //행의 상태 바꾸기, 비트마스크로 조합 표현, 조합에 의한 swap
if (i&(1 << j)) {
swapHT(0, j);
}
}
for (int j = 0; j < n; ++j) { //열의 상태 바꾸기, T가 H보다 많을 경우 swap
int sum = 0;
for (int k = 0; k < n; ++k) {
sum += b[k][j];
}
if (sum > n - sum) swapHT(1, j);
}
int sum = 0;
for (int j = 0; j < n; ++j) for (int k = 0; k < n; ++k) sum += b[j][k];
if (ans > sum) ans = sum;
}
cout << ans;
}
1202 보석 도둑 : https://www.acmicpc.net/problem/1202
1. 보석을 기준으로 문제를 풀때// 각각의 보석이 어떤 가방에 들어가야 할지
비싼 보석부터 각 보석을 담을 수 있는 가방 중에서 사이즈가 가장 작은 가방에 넣어야 최적의 해가 가능하다.
고로 비싼 보석 순으로 정렬 후에
효율적으로 가방에 넣어야 한다.
보석의 수, 가방의 수 <= 300,000 이기 때문에
무식한 방법으로 풀 경우에 NxK = 900억, 900초가 걸릴 수 있다.
이를 위해 가방선택 시간을 O(K) 보다 단축시키는 효율적인 자료 구조가 필요하다.
1. 어떤 수 X보다 큰 숫자 중에 가장 작은 수를 찾을 수 있는 Lower Bound
2. 구조를 유지하며 자료를 지울 수 있는 Erase
Balanced_BST(균형 이진 트리) 자료구조를 사용한다.
시간복잡도 : O(NlogN) + O(NlogK) // 보석 정렬 + 보석 선택 x(가방 선택, 가방 삭제)
#include <vector>
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
int n, k;
struct crystal {
int size, value;
};
int main(void) {
scanf("%d %d", &n, &k);
vector<crystal> v(n);
for (int i = 0; i < n; ++i) {
scanf("%d %d", &v[i].size, &v[i].value);
}
sort(v.begin(), v.end(), [](const crystal &a, const crystal &b) {
if (a.value == b.value) {
return a.size > b.size;
}
else return a.value > b.value;
});
multiset<int> bag;
for (int i = 0; i < k; ++i) {
int num;
scanf("%d", &num);
bag.insert(num);
}
long long sum = 0;
for (int i = 0; i < n; ++i) {
auto it = bag.lower_bound(v[i].size);
if (it != bag.end()) {
sum += v[i].value;
bag.erase(it);
}
}
printf("%lld", sum);
}
2. 가방을 기준으로 문제를 풀때// 각각의 가방에 어떤 보석이 들어가야 할지
가방과 보석을 무게를 기준으로 정렬하면
(1, 23), (2, 99), 2, (5, 65), 10
각 가방앞에 있는 보석들은 가방에 들어갈 수 있는 후보이다.
앞에서부터 가방에 보석을 넣는다고 할 때 가장 가격이 큰 보석을 넣으면 된다.
이를 위해 자료구조는 우선순위 큐를 사용하였다.
시간복잡도 : O((N+K)logN)
#define _CRT_SECURE_NO_WARNINGS
#include <vector>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
struct crystal {
int m, v=0, b = 0;
};
int main(void) {
int n, k;
scanf("%d%d", &n, &k);
vector<crystal> a(n + k);
for (int i = 0; i < n; ++i) scanf("%d%d", &a[i].m, &a[i].v);
for (int i = 0; i < k; ++i) {
scanf("%d", &a[n + i].m);
a[n + i].b = 1;
}
sort(a.begin(), a.end(), [](const crystal &n1, const crystal &n2) {
return (n1.m < n2.m || n1.m == n2.m && n1.b < n2.b);
});
long long ans = 0;
priority_queue<int> q;
for (auto &p : a) {
if (p.b == 0) {
q.push(p.v);
}
else {
if (!q.empty()) {
ans += (long long)q.top();
q.pop();
}
}
}
printf("%lld", ans);
}'Algorithm > Intermediate' 카테고리의 다른 글
| 이분탐색 문제 풀이[Binary Seach PS] (0) | 2021.08.24 |
|---|---|
| 분할 정복법(Divide and Conquer)(이분 탐색, 퀵 소트, 퀵 셀렉트, 머지 소트(병합 정렬))(Binary Search, Quick Sort, Quick Select, Merge Sort) (2) | 2021.08.05 |
| 너비 우선 탐색(BFS, Breadth First Search) (0) | 2021.06.06 |
| 브루트포스[2] - 재귀 함수 (2) | 2021.04.16 |
| 브루트포스[3]:백트레킹(backtracking) (0) | 2021.04.16 |


