암호학에서의 브루트 포스(brute force attack)가 아닌
알고리즘의 브루트 포스(brute force search)에 관한 것을 작성한다.
브루트 포스(brute force)
brute: 무식한, force: 힘
무식한 힘으로 해석되며 즉, 무식하게 다해보는 것이다.
완전탐색 알고리즘: 가능한 모든 경우의 수를 모두 탐색하면서 요구조건에 충족되는 결과만을 가져온다.
이 알고리즘의 강력한 점은 예외 없이 100%의 확률로 정답만을 출력한다.
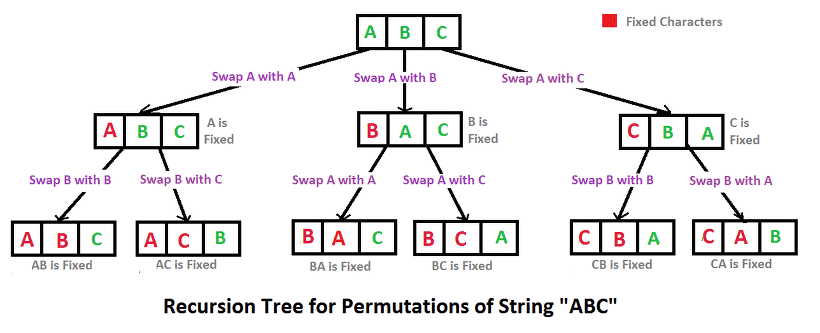
이러한 브루트 포스방법 중에서 순열에 관해서 소개를 하려고 한다.
순열(permutation)
수학에서, 순열 또는 치환은 서로 다른 n개의 원소에서 r(≤n)개를 뽑아 한 줄로 세우는 경우의 수이며, nPr로 나타낸다. 순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다. 즉, 순열은 정의역과 공역이 같은 일대일 대응이다. n개의 원소의 순서를 뒤섞는 순열의 개수는 n의 계승 n!와 같다. 즉, n 이하의 양의 정수들을 곱한 값이다.
브루트포스에서 순열은 순서와 관련된 경우, 선택과 관련된 경우, 그수가 고정된 경우 사용된다.
또한 아래의 모든 문제는 재귀함수를 사용해서 풀이가 가능하다.
순열과 관련된 함수
std::next_premutation
#include <algorithm>
default:
template <class BidirectionalIterator>
bool next_permutation (BidirectionalIterator first,
BidirectionalIterator last);
custom:
template <class BidirectionalIterator, class Compare>
bool next_permutation (BidirectionalIterator first,
BidirectionalIterator last, Compare comp);
std::next_premutation사용방법
범위내의 요소를 사전순으로 큰 순열로 재 배열한다.
반환값은 함수가 객체를 사전순으로 큰 순열로 재 배열 할 수있는 경우는 true를 반환하고 나머지는 false를 반환한다.
// next_permutation example
#include <iostream> // std::cout
#include <algorithm> // std::next_permutation, std::sort
int main () {
int myints[] = {1,2,3};
std::sort (myints,myints+3);
std::cout << "The 3! possible permutations with 3 elements:\n";
do {
std::cout << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '\n';
} while ( std::next_permutation(myints,myints+3) );
std::cout << "After loop: " << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '\n';
return 0;
}
/* out put
The 3! possible permutations with 3 elements:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
After loop: 1 2 3
out put */
// next_permutation example
#include <iostream> // std::cout
#include <algorithm> // std::next_permutation, std::sort
#include <vector> // std::vector
using namespace std;
int main() {
vector<int> myints = { 1,2,3 };
sort(myints.begin(), myints.end());
cout << "The 3! possible permutations with 3 elements:\n";
do {
cout << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '\n';
} while (std::next_permutation(myints.begin(), myints.end()));
cout << "After loop: " << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '\n';
return 0;
}
/* out put
The 3! possible permutations with 3 elements:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
After loop: 1 2 3
out put */
std::next_premutation주의할점
배열또는 벡터의 크기를 원소의 수만큼 맞춰야 한다.
불필요한 0등이 들어갈 경우에 모든 원소를 포함해서 순서쌍 순열을 만들기 때문에 원하지 않은 결과가 나온다.
순열과 관련된 문제
부등호-2529
설명 :
부등호 기호 <와 >가 나열된 수열 A가 있다.
기호의 앞뒤에 한자리 숫자를 넣어서 모든 부등호 관계를 만족시키려고 한다.
이때, 선택된 수는 모두 달라야 한다.
k개의 부등호 관계를 모두 만족시키는 (k+1)개 자리의 정수 중에서 최대값과 최소값을 구하는문제
풀이 :
전체 경우의 수는 10개의 수 중에서 k+1개를 고름, (k+1)! 순서를 모두 만들고 부등호 검사
하지만 전체 다해볼 필요 없이 큰자리, 작은자리 숫자를 고른후 배열만 신경쓰면 된다.
(큰 수, 작은 수 만가지고도 만족시키는 경우를 뽑아낼 수 있기 때문이다.)
즉, (k+1)!*(k+1)
#include <iostream>
#include <vector>
#include <cstdio>
#include <algorithm>
using namespace std;
int k;
bool check(vector<int> &v, vector<char> &ch) {
for (int i = 0; i < k; ++i) {
if (ch[i] == '<' && v[i] > v[i + 1]) {
return false;
}
if (ch[i] == '>' && v[i] < v[i + 1]) {
return false;
}
}
return true;
}
int main(void) {
scanf(" %d", &k);
vector<char> f(k);
vector<int> small(k+1);
vector<int> big(k+1);
for (int i = 0; i < k; ++i) scanf(" %c", &f[i]);
for (int i = 0; i <= k; ++i) {
small[i] = i;
big[i] = 9 - i;
}
do {
if (check(big, f)) {
for (int i = 0; i <= k; ++i) cout << big[i];
cout << endl;
break;
}
} while (prev_permutation(big.begin(), big.end()));
do {
if (check(small, f)) {
for (int i = 0; i <= k; ++i) cout << small[i];
cout << endl;
break;
}
} while (next_permutation(small.begin(), small.end()));
return 0;
}
단어수학-1339
풀이 : 모든 순서를 조사하는 방법으로 풀었음. //c++, 자바, 파이썬 중에서 파이썬은 시간이 오래걸려서 이방법으로 풀수 없다.
이 문제는 그리디방법으로 풀어도 되는 좋은 문제입니다.
아래 코드에서 벡터 A의 중복제거를 위해 erase와 unique를 사용했다.
A.erase(unique(A.begin(), A.end()), A.end())
계산을 하기 위해서 alpha배열을 사용했다.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <cstdio>
using namespace std;
int alpha[256];
int calc(vector<string> &str, vector<char> &ch, vector<int> &num) {
int m = ch.size();
for (int i = 0; i < m; ++i) {
alpha[ch[i]] = num[i];
}
int n = str.size();
int sum = 0;
for (string s : str) {
int now = 0;
for (char x : s) {
now = now * 10 + alpha[x];
}
sum += now;
}
return sum;
}
int main(void) {
int n;
cin >> n;
vector<string> str(n);
vector<char> ch;
for (int i = 0; i < n; ++i) {
cin >> str[i];
for (char x : str[i])
ch.push_back(x);
}
sort(ch.begin(), ch.end());
ch.erase(unique(ch.begin(), ch.end()), ch.end());
int m = ch.size();
vector<int> num(m);
for (int i = 0; i < m; ++i) num[i] = 9 - i;
sort(num.begin(), num.end());
int ans = 0;
do {
int sum = calc(str, ch, num);
if (ans < sum) ans = sum;
} while (next_permutation(num.begin(), num.end()));
cout << ans;
return 0;
}
14888
중복된 수가 있어서 (n-1)!*(n-1)가 아니라(겹치는 연산자가 있어서 실제로 더 적은 경우의 수이다. ) 더 작은수의 경우의수를 모두해본다.
민&맥스 함수 및 활용법 소개
연산자 벡터에 각각의 연산자를 연산자 개수만큼 넣는다.
결과값을 벡터에 저장후 이런식으로도 할수 있다.
내 제출코드 : http://boj.kr/4a0b62d59e774fae9ddb99ec876a661d
스타트와링크14889
N/2라는 말이 없으면 순열을 이용해서 풀수없다.
1팀의 수와 2팀의 수를 알수없기 때문이다.
전체경우의수는 20C10 = 20!/10!*10! =184756, 즉 전부다해도 된다.
선택과 관련된 문제인데 선택해야되는것의 개수가 정해져있다면 순열을 이용해도 된다.
'Algorithm > Intermediate' 카테고리의 다른 글
| 너비 우선 탐색(BFS, Breadth First Search) (0) | 2021.06.06 |
|---|---|
| 브루트포스[2] - 재귀 함수 (2) | 2021.04.16 |
| 브루트포스[3]:백트레킹(backtracking) (0) | 2021.04.16 |
| 비트마스크(BitMask) (1) | 2021.04.14 |
| 깊이 우선 탐색(DFS, Depth-First Search) (0) | 2019.05.02 |


